符号简述#
和 分别表示实数域和复数域, 和 分别表示整数和非负整数, 表示正整数。
对 ,定义 个复平面的笛卡尔积为 维复数空间
其具有自然的 维复向量空间结构。 上的标准 Hermite 内积为
该内积产生的范数 诱导出了 中的欧氏距离
为与一维复空间的 书写形式统一,对 ,也记 。
与 R²ⁿ 的联系#
定义以 为圆心, 为半径的开球为
设 ,记 ,则映射
是 到 的一个实线性同构,且对 上的 L-2 范数有 ,所以 为 上以 为圆心, 为半径的开球,即 与 拓扑同胚。
由此可将 中的拓扑、分析的通常概念替换到 中。
基础概念#
-
开集:设 为一点集,若 ,,使得 ,则称 为开集。
-
连通集:设 为一点集,若 不能表示为两个非空开集之并,则称 是连通的。
-
区域:连通的开集。
-
相对紧子集:设 为一子集,若其闭包 ,则称 为 的一个相对紧子集,记为 。
-
多圆柱:
定义以 为圆心, 为(多)半径的开多圆柱为
其为 中 个开圆盘的笛卡尔积。
-
多圆域:
更一般地,称 个复平面区域 的笛卡尔积 为一个多圆域。
点集 的拓扑边界记为
绝对空间#
称映射 为绝对空间, 中点集在绝对空间下的像可更为方便地用几何表示。
例如,容易画出 和 在绝对空间的图形如下:
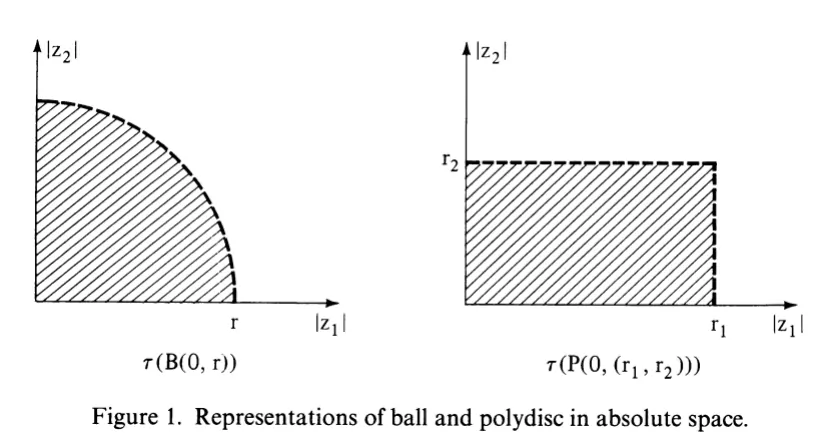
Hartogs 图形#
当 时,为简化书写,通常记 ,其中 。
设 满足 ,定义区域
则 的图形可表示如下:
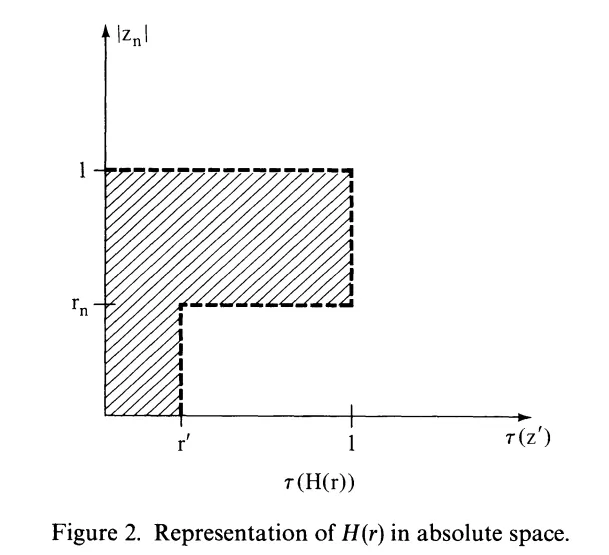
称 这样的一个「对」为一个(欧式)Hartogs 图形。
Reinhardt 域#
注意对 而言,
是一个 维的实环面1。因此有如下定义:
设 为一点集,若 ,环面
也落在 内,则称 是圆形的。在 中,只有圆形点集的绝对空间表示才是有意义的。
设 为以原点为中心的开圆形域,则称 为 Reinhardt 域。若 还满足 ,均有 ,则称 是完备的。 和 是完备的 Reinhardt 域,但是 是不完备的 Reinhardt 域。
考虑全纯函数的洛朗级数展开时就会遇到 Reinhardt 域, 中典型的完备 Reinhardt 域是以原点为圆心的开圆盘,而典型的不完备 Reinhardt 域是以原点为圆心的圆环区域。


