本文基于考研 408 的 KMP 算法编写。

KMP 算法核心思想：主字符串指针只进不退

KMP 匹配算法

这个比较简单，基于 next 数组进行计算即可。

匹配使用双指针进行，主字符串的指针只进不退，当模式串指针指向的字符与主字符串指针指向的字符匹配时，两个指针一起 +1；当模式串的某个字符不匹配时，则根据 next 数组中的对应值，将模式串指针移动到相应的地方。直接看代码更简单：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
std::optional<size_t> kmpMatch(const std::string& str, const std::string& pattern) {
    if (pattern.empty()) {
        return 0;
    }
    std::vector<size_t> next = generateNext(pattern);
    // pattern无符号，需要额外+1来处理首字符不匹配的情况
    size_t str_ptr = 0, pattern_ptr = 1;
    while (str_ptr < str.size() && pattern_ptr <= pattern.size()) {
        if (pattern_ptr == 0 || str[str_ptr] == pattern[pattern_ptr - 1]) {
            // 匹配时，指针都后移
            str_ptr++;
            pattern_ptr++;
        } else {
            // 不匹配时，模式串指针回到next数组中对应位置
            pattern_ptr = next[pattern_ptr - 1];
        }
    }
    if (pattern_ptr > pattern.size()) {
        // 匹配成功，返回匹配的首个字符位置
        return str_ptr - (pattern_ptr - 1);
    } else {
        // 匹配失败，返回空
        return {};
    }
}

KMP next 数组生成算法

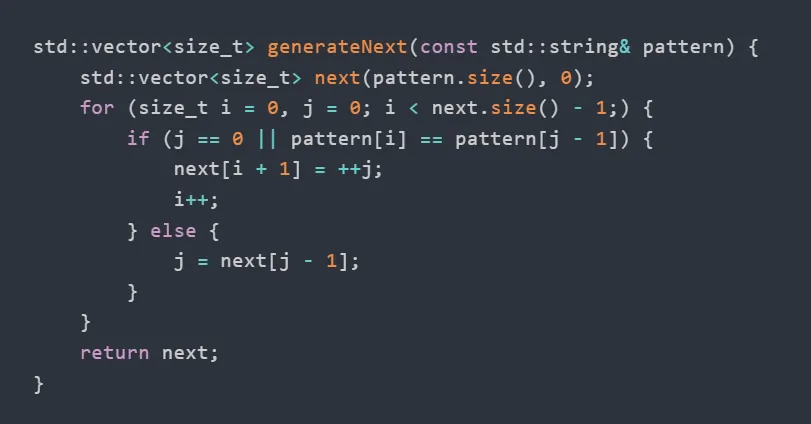
这个才是重中之重。先上算法代码： 

1
2
3
4
5
6
7
8
9
10
11
12
std::vector<size_t> generateNext(const std::string& pattern) {
    std::vector<size_t> next(pattern.size(), 0);
    for (size_t i = 0, j = 0; i < next.size() - 1;) {
        if (j == 0 || pattern[i] == pattern[j - 1]) {
            next[i + 1] = ++j;
            i++;
        } else {
            j = next[j - 1];
        }
    }
    return next;
}

以下为叙述方便起见，采用类似 MATLAB 的 str[a:b] 的形式来表示 str.substr(a, b - a) 这一子串。

算法的输出 next 数组中，next[i] 对应的是 pattern[0:i - 1] 的最长公共前后缀长度 +1。算法的循环可以看作两个部分，一个部分是递增 i，而另一个循环则是移动 j 来找到 pattern[0:i] 的最长公共前后缀长度，所以每次 i++ 后，j 都表示 pattern[0:i - 1] 的最长公共前后缀长度 +1(因为 j 也跟着递增了)。

着重考虑第二个循环，即 i++ 后移动 j 的部分。循环开始时，比较 pattern[0:i] 后缀的最后一个字符，即 pattern[i] ，与 pattern[0:i - 1] 的最长公共前后缀所对应前缀的下一个字符，即 pattern[j - 1] 是否相等。

如果相等，就说明 pattern[0:i] 的最长公共前后缀为 pattern[0:j - 1] 和 pattern[i - j:i]，因为 pattern[0:i - 1] 的最长公共前后缀恰为 pattern[0:j - 2] 和 pattern[i - j:i - 1]。

如果不相等，则回退 j。这是因为 pattern[0:j - 2] == pattern[i - j:i - 1]，而 next[j - 1] 就是 pattern[0:j - 2] 的最大公共前后缀长度 +1，也是 pattern[i - j:i - 1] 的最大公共前后缀长度 +1，所以要把 j 回退到 next[j - 1]。

换句话来说，第二个循环就是利用已经计算好的公共前后缀长度与前后缀相同的性质，按顺序不断尝试寻找最长的公共前后缀，如果发现前后缀不匹配，就回退到次长公共前后缀继续尝试寻找，直到 j 回退到 pattern[0]，也就是找不到任何公共前后缀时循环结束，递增 i。

KMP nextval 数组

在 KMP 的匹配算法中，如果 pattern[i] 失配，则模式串指针回退到 next[i] - 1 处。但如果 pattern[i] = pattern[next[i] - 1]，那回退后进行的下一次匹配一定是失配的，还要继续回退，相当于进行了一次无用的匹配。

nextval 就是用来解决这个问题的，在计算出 next 数组后，再遍历 next 数组做一次修改，如果 pattern[i] = pattern[next[i] - 1]，就让 next[i] = next[next[i] - 1]，省去一次无用的跳转。

算法代码如下：

1
2
3
4
5
6
7
8
9
10
11
void generateNextval(const std::string& pattern, std::vector<size_t>& next) {
    if (next.size() == 0) {
        return;
    }
    for (size_t i = 1; i < pattern.size(); ++i) {
        if (pattern[i] == pattern[next[i] - 1]) {
            next[i] = next[next[i] - 1];
        }
    }
    return;
}