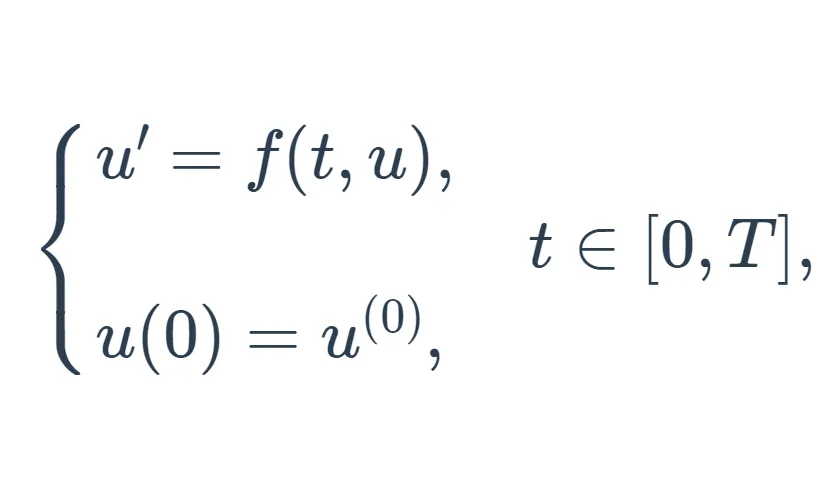向前欧拉、向后欧拉、跃点（蛙跳）、梯形四种有限差分方法的准确性（收敛性）、稳定性数学推导

NOTE

本文由以前的课程论文使用 pandoc 转换到 markdown 博客，原文为本人厦门大学数学系课程《微分方程数值解》的课程论文，参考时请注意。

简介#

本文默认读者对有限差分方法有一定了解，因此不做过多的前置知识介绍。

考虑如下初值问题:

将划分为个等距区间，，我们有以下几种有限差分格式用于求其数值解:

向前欧拉格式

向后欧拉格式

跃点(Leap frog)格式

梯形格式

接下来，对以上四种有限差分格式，我们将进行其准确性(Accuracy)与稳定性(Stability)的数学推导。

准确性推导#

首先定义局部截断误差(Local Truncation Error) ，其定义为：其他点处的精确解在处按照差分格式计算得到的结果与处的精确解的差值。

WARNING

上述局部截断误差与通常定义的局部截断误差相差一个，参考时请注意。

向前欧拉格式#

向前欧拉格式的局部截断误差可表示为如下等式

对进行 Taylor 展开有

于是有

误差可表示为如下形式：

令，对误差有如下估计：

向后欧拉格式#

向后欧拉格式的局部截断误差可表示为如下等式

对进行 Taylor 展开有

于是有

误差可表示为如下形式：

令，假定，对误差有如下估计：

跃点格式#

跃点格式的局部截断误差可表示为如下等式

对和进行 Taylor 展开有

于是有

误差可表示为如下形式：

令，对误差有如下估计：

令，，则，且 . 于是上式可改写为如下形式：

不妨假定上式中的是由向前欧拉格式得到的，注意到时，于是有

梯形格式#

跃点格式的局部截断误差可表示为如下等式

对和进行 Taylor 展开有

于是有

误差可表示为如下形式：

令，假定，对误差有如下估计：

稳定性推导#

考虑模型问题

其中为常数。定义为舍入误差，. 我们称差分格式的绝对稳定区域(Absolute Stability Region)为复平面上所有使差分格式的解稳定的的集合。

向前欧拉格式#

将格式代入模型问题可得

考虑到舍入误差，我们有而非：

误差满足

假设，若，则有

其中为常数，所以本格式的绝对稳定区域为 .

向后欧拉格式#

将格式代入模型问题可得

考虑到舍入误差，我们有而非：

误差满足

假设，若，则有

其中为常数，所以本格式的绝对稳定区域为 .

跃点格式#

将格式代入模型问题可得

考虑到舍入误差，我们有而非：

误差满足

其中，多值函数取将正数映射到正数的解析分支。随后我们有

假设，若，则有

上式同时出现与，所以仅时跃点格式稳定。令有

其中

注意到仅且时上式成立，所以跃点格式的绝对稳定区域为 .

梯形格式#

将格式代入模型问题可得

考虑到舍入误差，我们有而非：

误差满足

假设，令，若，则有

其中为常数，所以本格式的绝对稳定区域为 .

数值试验#

四种有限差分格式的MATLAB代码

向前欧拉格式：

function [x, result] = forward_euler(T, step, u0, f)
    x = linspace(0, T, step + 1);
    h = T / step;
    result = zeros(1, step + 1);
    result(1) = u0;
    for k = 2:step + 1
        result(k) = result(k - 1) + h * f(x(k - 1), result(k - 1));
    end
end

matlab

向后欧拉格式：

function [x, result] = backward_euler(T, step, u0, f)
    x = linspace(0, T, step + 1);
    h = T / step;
    result = zeros(1, step + 1);
    result(1) = u0;
    for k = 2:step + 1
        temp_func = @(uk) result(k - 1) + h * f(x(k), uk) - uk;
        result(k) = fzero(temp_func, result(k - 1));
    end
end

matlab

跃点格式：

function [x, result] = leap_frog(T, step, u0, u1, f)
    x = linspace(0, T, step + 1);
    h = T / step;
    result = zeros(1, step + 1);
    result(1) = u0;
    result(2) = u1;
    for k = 3:step + 1
        result(k) = result(k - 2) + 2 * h * f(x(k - 1), result(k - 1));
    end
end

matlab

梯形格式：

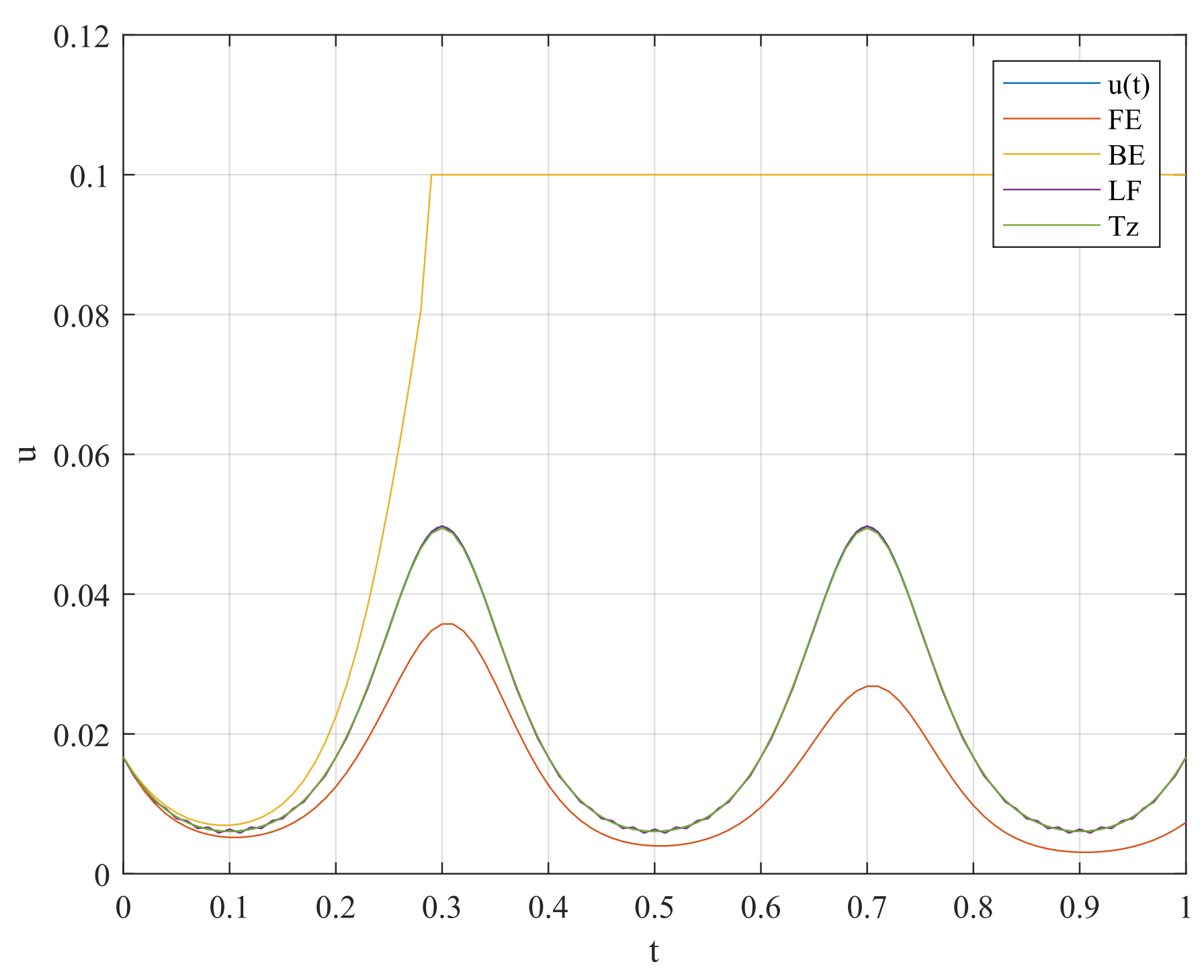
function [x, result] = trapezoidal(T, step, u0, f)
    x = linspace(0, T, step + 1);
    h = T / step;
    result = zeros(1, step + 1);
    result(1) = u0;
    for k = 2:step + 1
        temp_func = @(uk) result(k - 1) - uk + ...
            h * (f(x(k), uk) + f(x(k - 1), result(k - 1))) / 2;
        result(k) = fzero(temp_func, result(k - 1));
    end
end

matlab

考虑如下初值问题：

其解析解为：

使用上述代码进行有限差分求解，得到数值结果如下：

数值结果